Nyquist Is Not Broken!
I’ve been following a conversation at another site for the past week or so. I’m content standing on the sidelines while a couple of authorities beat up on each other. What they’re arguing about comes down to theory vs. practice. The respective posts stake out contrary positions on the merits of the Shannon-Nyquist Theorem AKA The Sampling Theorem. The practical engineer (and individual with plenty of experience and knowledge about building high-end audio circuits) contends that the Nyquist Theorem is broken. The other expert addressed the issue from a theoretical position and is emphatic that the Nyquist Theorem is not broken. So who’s actually right? Is the notion that a continuous analog waveform can be properly sampled “only if it does not contain frequency components above one-half of the sampling rate” true or false?
Let’s start with the definition of proper sampling. It’s actually pretty straightforward. If we sample a continuous signal in some fashion and then can precisely reconstruct the analog signal from the samples we took, then we must have done the sampling properly. Regardless of whether the input signal is a pure sine wave or a complex tone, if we can reproduce the source analog signal from the samples, then we’ve properly sampled the original source.
That’s the theory and it’s still true no matter what the engineers and designers of the world say to the contrary. But there are some real world considerations that must be take into account. So I thought it might be beneficial to explore the Nyquist Theorem once again.
Here are some cases that should help to clarify the basic concepts of The Sampling Theorem. This is the theory part of the discussion. I’ve placed four sine waves that illustrate the relationship between the source analog signal and the digitized version in the figures below.
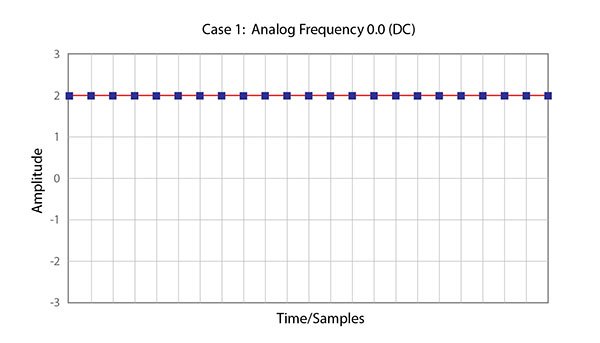
Figure 1 – An analog signal that is a constant DC value, a cosine wave of zero frequency.
This is a properly sampled continuous signal, although one that has no frequency. It is a simple steady state DC offset that can be described by a series of straight lines between each of the samples. Thus all of the information needed to reconstruct the analog signal is contained in the digital data. Clearly, this unique signal is represented 100% by the samples.
Now take a look at a periodic waveform.
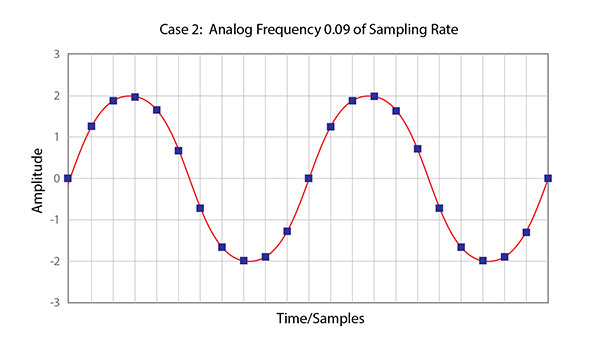
Figure 2 – This illustration shows a sine wave with a frequency that is .09 or 9% of the sampling rate.
The sine wave shown in Figure 2 has a frequency that is 9% of the sampling rate. This might represent, for example, a 900 cycles/second sine wave being sampled at 10,000 Hz. In other words, there are 11.1 samples taken over a single cycle of the wave. This situation is more complex than the previous case. A straight line doesn’t exist between the sample values. So the question is, do the samples accurately represent the original source sine wave? The answer is yes, because no other sine wave, or combination of sine waves, will produce this pattern of samples. These samples correspond to only one analog signal and therefore the analog signal can be exactly reconstructed. This is proper sampling once again.
It’s pretty clear that the sine wave is identified clearly in the samples of Figure 2. But what happens when the frequency of the source is substantially higher?
Come back tomorrow and we’ll take a look.
+++++++++++++++++++
I’m still looking to raise the $3700 needed to fund a booth at the 2015 International CES. I’ve received some very generous contributions but still need to raise additional funds (I’ve received just under $2000). Please consider contributing any amount. I write these posts everyday in the hopes that readers will benefit from my network, knowledge and experience. I hope you consider them worth a few dollars. You can get additional information at my post of December 2, 2014. Thanks.


Mark, you’re probably going to cover this tomorrow, but shouldn’t it be “no other sine wave, or combination of sine waves with frequencies less than half the sampling frequency”?
Stay tuned…
It’s just like Wikipedia says:
If a function x(t) contains no frequencies higher than B cps, it is completely determined by giving its ordinates at a series of points spaced 1/(2B) seconds apart.
A sufficient sample-rate is therefore 2B samples/second, or anything larger. Conversely, for a given sample rate fs the bandlimit for perfect reconstruction is B ≤ fs/2 . When the bandlimit is too high (or there is no bandlimit), the reconstruction exhibits imperfections known as aliasing. Modern statements of the theorem are sometimes careful to explicitly state that x(t) must contain no sinusoidal component at exactly frequency B, or that B must be strictly less than ½ the sample rate. The two thresholds, 2B and fs/2 are respectively called the Nyquist rate and Nyquist frequency. And respectively, they are attributes of x(t) and of the sampling equipment. The condition described by these inequalities is called the Nyquist criterion, or sometimes the Raabe condition.
(You can’t selectively excerpt bits from a theory that as part of the theory says other conditions must be fulfilled and then criticise the excerpt)
Thanks for the comment…I’m getting there. Stay tuned.
I have heard this claim before. The claim seems to imply that when there is information in the music signal above Fs/2, then sampling at Fs does not even correctly replicate the signal below Fs/2.
If true, the claim would indeed say that digital audio doesn’t work.
Looking forward to your common-English resolution.
I see MFSL will be debuting new hybrid SACD/CD’s at CES that are mastered from quad dsd transferred analog tapes. Clearly there is an industry move to higher and higher sampling rates.
Which is more hocus pocus marketing spin.
Ignoring the mathematically trivial case in Figure 1 and the “obvious” sine wave case in Figure 2, perhaps the question should be what happens with a complex waveform made up of lots of superposed waveforms, ie a real-world sample of music?
Dave…be patient. I’m writing a series of posts that will address your question. I want to make it clear that a set of sample points that fall within the criteria of The Sampling Theorem can describe accurately a continuous waveform. As we will see, there is no requirement that the signal be a pure sine wave.
Thanks, I eagerly await your post.
Hi,
I have a question.
I figure since in a stereo recording one sound event could arrive at one of the microphones less than 1/44100 seconds later than the other and IIRC the smallest detectable interaural time difference is roughly half that figure, could this make an audible difference when moving to higher sampling frequencies? Would make sense, since audiophiles often talk about higher-res recordings sounding more “three dimensional”.
Thank you.
There are some current questions regarding the acuity of human hearing with regards to the time domain. I’ve read papers that say that 5 to 10 microseconds is required and others that say 8 microseconds is below our ability to hear it. I feel confident that 96 kHz or 192 kHz can deliver true fidelity. If signals are presented to your 44.1 kHz system that are faster than 22.050 kHz they will be filtered out to avoid aliasing or they will distort the reproduced signal…according to Nyquist.
Quite a few audiophiles are aware of that research finding about hearing timing differences, and they are confusing it with a need to sample at that rate. Digital timing accuracy is within a few nanoseconds, even at low sampling rates. There is no relation between the research and sampling rate.
Thanks Grant…I’ll be addressing this asap. I received a very informative email from some an engineer at B&W about higher sample rates and timing.
I’m slightly confused. You say only one sine wave could fit those points, which is fine.
But I’m wondering….so what? How does that matter in terms of reconstruction of the wave at the end? Surely there isn’t some computer sitting there trying out different waves and then only outputting the one that fits? So how does it actually work?
Also, what about for complex waveforms that are not easily predictable like a sine is?
Thanks