Aliasing and Foldover: A Primer

Have you heard of “aliasing” or “foldover”? In a nutshell, these terms describe another potential problem area for PCM digital audio. We’ve talked about quantization noise and jitter in the past but I don’t think that I’ve explored the concept of aliasing. Consider today’s post an introduction to aliasing…or what happens when a frequency that is higher than half the sample rate reaches your analog to digital converter.

The catalyst for today’s post came from yesterday’s post. As you may recall (you can click here to read it), I did some spectra analysis of a DXD download and found the same sort of ultrasonic noise that is typical of 1-bit DSD type encoding…even though DXD is multibit PCM. The post I wrote about demo files also inspired today’s post (click here to revisit that post). The spectra associated with most of the music bundled with a new high-resolution audio smartphone were full of unwanted ultrasonic noise. It turns out that the “out of band” noise that is unavoidable when recording and releasing music in DSD (even music that is then transcoded to high-resolution PCM) can be a very bad thing for a playback device. We’ll get that story tomorrow.

First, we need to understand that there are some very rigid boundaries associated with digitizing audio. One of them is defined by the Nyquist frequency, which is equal to half of the sample rate. For example, if we take the 44.1 kHz sample rate of a Redbook CD, the Nyquist frequency is 22.050 kHz. That’s the absolute maximum frequency that can be captured by a PCM-based system…and that’s under ideal conditions. But what happens if a frequency of 25 kHz comes along. What does the AD converter do? It tries to digitize it. But it turns out that it doesn’t have enough samples available to do it correctly.

A PCM system needs at least 2 samples for each cycle of a signal. They don’t have to match the top and bottom of the periodic waveform (a common mistake), but the converter does need 2 samples. Let’s take a look at an illustration that shows this:

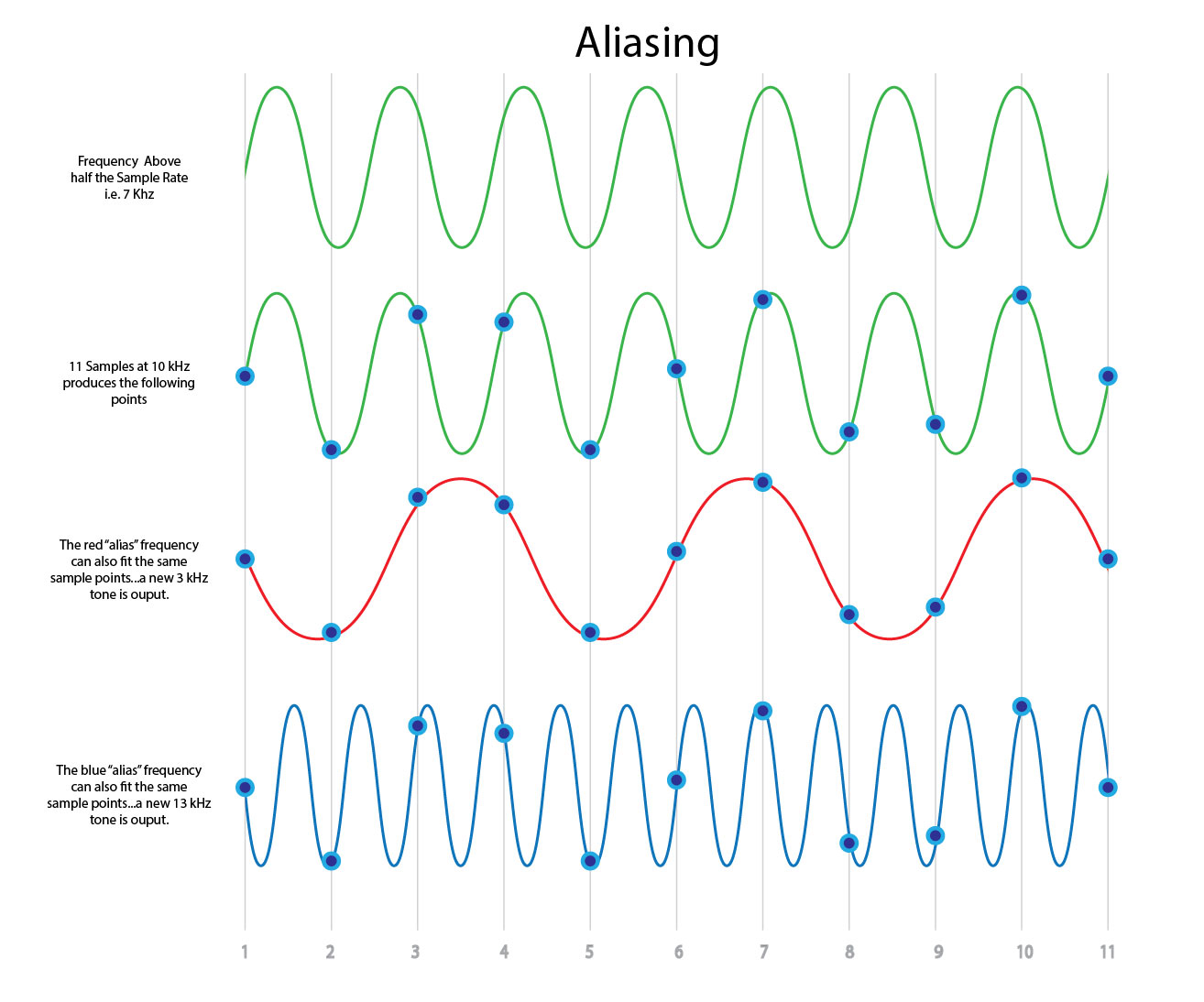
Figure 1 – A series of waveforms showing a 7 kHz and 13 kHz tone sampled in a 10 kHz system with the resulting “alias tones” that are generated and output. [Click to enlarge]

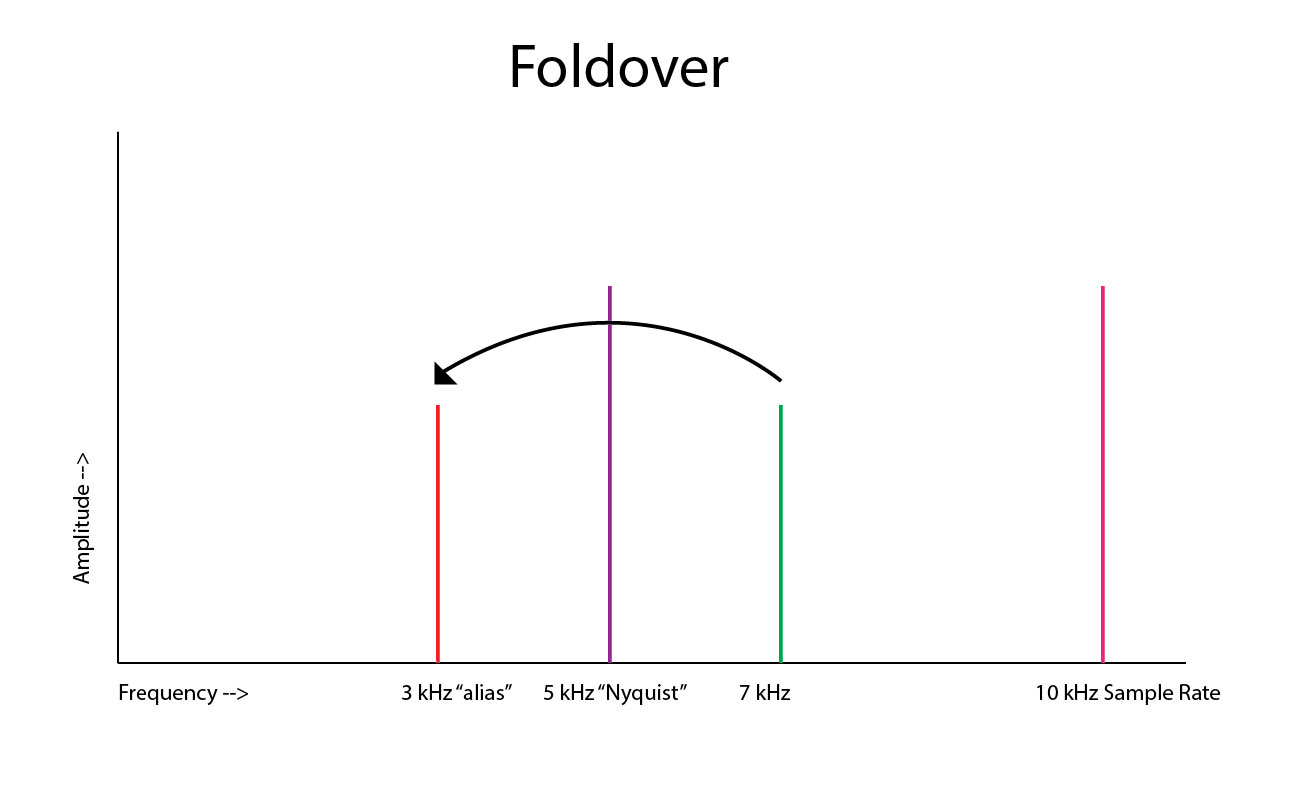
Any frequency presented to an AD converter that is higher than half of the sampling rate cannot be accurately captured and a false frequency called an “alias” is stored or output instead. The green waveform is what we want but the 7 kHz tone is higher than 5 kHz (the Nyquist frequency or half the sample rate of 10 kHz). So the red 3 kHz alias tone is output as is the 13 kHz blue tone. This is obviously a problem and results in foldover. We could filter out the 13 kHz tone at the DAC but the 3 kHz tone is in the middle of the sound we want! Here’s another illustration:

Figure 2 – An illustration showing how the 7 kHz frequency “folds over” around the Nyquist causing a tone that doesn’t belong. [Click to enlarge]

So there you have it. And that’s why AD converters have very precise Low Pass Filters to make sure that any frequency that is greater than the sample rate divided by 2 is never allowed to arrive at the digitizer.

Tomorrow, I’ll talk about the real world and how aliasing can be our friend or out enemy.